Question

in a random sample of 200 people, 154 said that they watched educational television. fine the 90% confidence interval of the true proportion of people who watch educational television. if the television company wanted to publicize the proportion of viewers, do you think it should use the 90% confidence interval?

Answer 1

[0.7210,0.8189] = [72.10%, 81.89%]

Explanation:

The sample size is

n = 200

the proportion is

p = 154/200 = 0.77

Since both np ≥ 10 and n(1-p) ≥ 10

We can approximate this discrete binomial distribution with the continuous Normal distribution. As the sample size is large enough, not applying the continuity correction factor makes no significant difference.

The approximation would be to a Normal curve with this parameters:

Mean

p = 0.77

Standard deviation

`\bf s=\sqrt{(p(1-p))/(n)}=\sqrt{(0.77*0.23)/(200)}=0.0298`

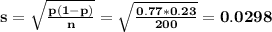
The 90% confidence interval for the proportion would be then

`\bf  [0.77-z^*0.0298, 0.77+z^*0.0298]`

where
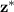`\bf z^*` is the 10% critical value for the Normal N(0,1) distribution , this is a value such that the area under the N(0,1) curve outside the interval
`\bf [-z^*,z^*]` is 10%=0.1

We can either use a table, a calculator or a spreadsheet to get this value.

In Excel or OpenOffice Calc we use the function

NORMSINV(0.95) and we get a value of 1.645

The 90% confidence interval for the proportion is then

`\bf  [0.77-1.645^*0.0298, 0.77+1.645^*0.0298]=[0.7210,0.8189]`

This means there is a 90% probability that the proportion of people who watch educational television is between 72.10% and 81.89%

If the television company wanted to publicize the proportion of viewers, do you think it should use the 90% confidence interval?

Yes, I do.