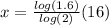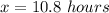The population of bacteria in a petri dish doubles every 16 h. The population of the bacteria is initially 500 organisms. How long will it take for the population of the bacteri…

Question

asked Sep 28, 2020 185k views

2 Answers

Tai Paul · Answer 1 · 2020-10-03T11:12:00+0000

Answer:

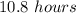
$10.8\ hours$

Explanation:

In this problem we have a exponential function of the form

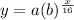
$y=a(b)^{(x)/(16)}$

where

y ---> is the population of the bacteria

x ---> the time in hours

a ---> is the initial value of the population

b ---> is the base

r ---> is the rate

b=(1+r)

where

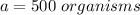
$a=500\ organisms$

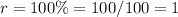
$r=100\%=100/100=1$

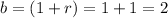
b=(1+r)=1+1=2

substitute

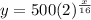
$y=500(2)^{(x)/(16)}$

so

For y=800

substitute and solve for x

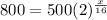
$800=500(2)^{(x)/(16)}$

$1.6=(2)^{(x)/(16)}$

Apply log both sides

$log(1.6)=log[(2)^{(x)/(16)}]$

log(1.6)={(x)/(16)}log(2)

x=(log(1.6))/(log(2))(16)

$x=10.8\ hours$