Answer:
NO
Explanation:
Let the consecutive numbers be x and x + 1
Given condition is their reciprocals sum is equal to 3/4

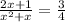
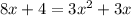

Find the discriminant for the above quadratic equation
Foe a given quadratic equation
 the discriminant =
the discriminant =
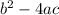
Here a = 3,b = -5,c = -4
Discriminant =
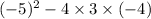 =78 >0
=78 >0
If a quadratic equation has discriminant > 0 it has distinct real roots
The roots are
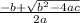 and
and
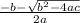
Here the roots are
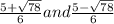
They are not integers So there are no consecutive pair of integers which follow the given condition