Question

If an object is projected upward with an initial velocity of 48 feet per second, at what times will it reach a height of 32 feet above the ground. Given h(t)=vt - 16t^2

Answer 1

t = 1s and t = 2s

Explanation:

We have the equation

`h(t)=vt - 16t^2`

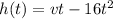
where
`v=48ft/s`

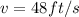
and
`h=32ft`

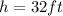
Thus, the equation now becomes:

`32=48t - 16t^2`

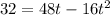
To solve, we must first equal the quadratic equation to zero

`- 16t^2+48t -32=0`

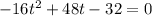
Solve this equation for t using the general formula for a quadratic equation

`x=(-b+-√( b^2-4ac) )/(2a)`

but in this case intead of x we have t.

`t=(-b+-√( b^2-4ac) )/(2a)`

Where a is the coefficient of the quadratic term.

b is the coefficient of the linear term, and c the independent term.

`a= -16\\b= 48\\c=-34`

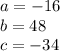
And now we substitute these values in the general formula:

`t=(-48+-√( 48^2-4(-16)(-32)) )/(2(-16))`

`t=(-48+-√( 2304-2048) )/(-32)`

`t=(-48+-√(256) )/(-32)`

`t=(-48+-16 )/(-32)`

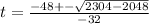
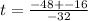
Now, we are going to have two values for t due to the +- sign. Using the negative sign:

`t=(-48-16 )/(-32)`

`t=2s`

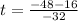
And using the positive sign:

`t=(-48+16 )/(-32)`

`t=1s`

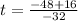
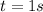
At times t = 1s and t = 2s the object will it reach a height of 32 feet above the ground.