What is the significance of the mean of a probability distribution?

Question

asked Sep 1, 2020 101k views

1 Answer

David Alber · Answer 1 · 2020-09-05T13:07:13+0000

Answer:

Significance of the mean of a probability distribution.

Explanation:

The mean of a probability distribution is the arithmetic average value of a random variable having that distribution.

For a discrete probability distribution, the mean is given by,
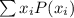$\sum x_iP(x_i)$ , where P(x) is the probabiliy mass function.
For a continuous probability distribution, the mean s given by,
$E(x) = \int x_if(x_i)$ , where f(x) is the probability density function.
Mean is a measure of central location of a random variable.
It is the weighted average of the values that X can take, with weights given by the probability density function.
The mean is known as expected value or expectation of X.
An important consequence of this is that the mean of any symmetric random variable (continuous or discrete) is always on the axis of symmetry of the distribution.
For a continuous random variable, the mean is always on the axis of symmetry of the probability density function.