Answer:
The probability of rolling a seven or rolling an even number as the sum of the two dice is

Explanation:
Given : Imagine you have a pair of six-sided dice.
To find : What's the probability of rolling a seven or rolling an even number as the sum of the two dice?
Solution :
Rolling a pair of six-sided dice,
(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)
Rolling a seven as the sum of the two dice are (1,6),(2,5),(3,4),(4,3),(5,2),(6,1)
Rolling an even number as the sum of the two dice are (1,1),(1,3),(1, 5),(2, 2),(2, 4),(2, 6) ,(3, 1),(3, 3),(3, 5),(4, 2),(4, 4),(4, 6),(5, 1),(5, 3),(5, 5),(6, 2),(6, 4),(6, 6).
Favorable outcome of rolling a seven or rolling an even number as the sum of the two dice are (1,6),(2,5),(3,4),(4,3),(5,2),(6,1), (1,1),(1,3),(1, 5),(2, 2),(2, 4),(2, 6) ,(3, 1),(3, 3),(3, 5),(4, 2),(4, 4),(4, 6),(5, 1),(5, 3),(5, 5),(6, 2),(6, 4),(6, 6) - 24
The probability is given by,
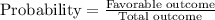
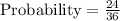
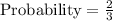
Therefore, the probability of rolling a seven or rolling an even number as the sum of the two dice is
