Answer:
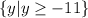
Explanation:
In a parabola there are two characteristics that help to find its range: vertex and the coefficient of the quadratic term.
So, the vertical coordinate of the vertex is the critic point of the range, it's part of the restriction. Then, we have to observe if the parabola is concave up or concave down. If the coefficient of the quadratic terms is positive, then the parabola is concave up, like this problem. All this means that the range valid for the function comprehend all real number major than -11, because the parabola is concave up.
Therefore, the right answer is third one.
(Function's graph is attached, there you can see that all range values are above y = -11)