Question

Rewrite the expression with rational exponents as a radical expression by extending the properties of integer exponents.

two to the three-fourths power, all over two to the one half power


the eighth root of two to the third power

the square root of two to the three-fourths power

the fourth root of two

the square root of two

Answer 1

yes, the the fourth root of two is correct

Explanation:

i just took the test today and got it correct

Answer 2

`\sqrt[4]{2}`

Explanation:

We start with the original problem:

`(2^(3/4))/(2^(1/2))`

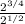
So first we start by applying the quotient rule for powers, which tells you that whenever you are dividing two powers that have the same base and different power, you can copy the base and subtract the powers:

`(b^(a))/(b^(c))=b^(a-c)`

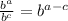
so:

`(2^(3/4))/(2^(1/2))=2^{(3)/(4)-(1)/(2)}`

which yields:

`2^{(1)/(4)}`

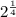
since we are talking about a rational exponent, we can next turn it into a radical by using the following rule:

`b^{(1)/(a)}=\sqrt[a]{b}`

so:

`2^{(1)/(4)}=\sqrt[4]{2}`