Question

Starting from rest at t = 0 s, a wheel undergoes a constant angular acceleration. When t = 3.8 s, the angular velocity of the wheel is 4.8 rad/s. The acceleration continues until t = 20 s, when the acceleration abruptly changes to 0 rad/s2. Through what angle does the wheel rotate in the interval t = 0 s to t = 55 s?

Answer 1

Total displacement will be 1136.79 rad

Step-by-step explanation:

We have given that wheel starts from the rest so initial angular velocity
`\omega _0=0rad/sec`

Angular velocity after 3.8 sec is given as 4.8 rad/sec

So
`\omega _f=4.8rad/sec`

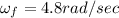
From second equation of motion we know that

`\omega _f=\omega _0+\alpha t`

`\alpha =(\omega _f-\omega _i)/(t)=(4.8-0)/(3.8)=1.2631rad/sec^2`

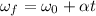
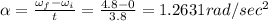
This acceleration is constant until 20 sec

So displacement in 20 sec

`\Theta =\omega _0t+(1)/(2)\alpha t^2=0* 20+(1)/(2)* 1.2631* 20^2=252.62rad`

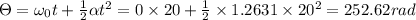
Total time is given as t = 55 sec

So left time = 55 - 20 =35 sec

After 20 sec angular acceleration is 0

So displacement in 35 sec

`Theta =\omega _0t`

Angular velocity after 20 sec
`\omega _0=\alpha t=1.2631* 20=25.262rad/sec`

So displacement
`\Theta =35* 25.262=884.17rad`

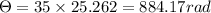
So total displacement in 55 sec = 252.62 +884.17 = 1136.79 rad