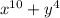Factor x^10 +y^4 using the sum of squares (hint: x^10 = (x^5)^2 and y^4 = (y^2)^2)

Question

asked Jan 17, 2020 88.2k views

1 Answer

Maxter · Answer 1 · 2020-01-20T19:41:19+0000

x^(10) +y^4 cannot be factorized that is cannot be represented as products of lower degree polynomials.

Solution:

Need to factor
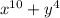x^(10) +y^4 using the sum of squares that is we need to factorize

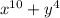
x^(10)+y^(4)=x^((5 * 2))+y^((2 * 2))

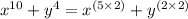
Using law of exponent
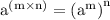
$\mathrm{a}^{(\mathrm{m} * \mathrm{n})}=\left(\mathrm{a}^{\mathrm{m}}\right)^{\mathrm{n}}$

On applying this we get,

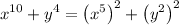
$x^(10)+y^(4)=\left(x^(5)\right)^(2)+\left(y^(2)\right)^(2)$

But there is no direct formula of
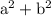$\mathrm{a}^(2)+\mathrm{b}^(2)$ which can provide factors.

Hence we can say that
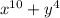x^(10) +y^4 cannot be factorize that is cannot be represented as products of lower degree polynomials.