Question

An equilateral triangle has sides of length(3k-2)units. A regular pentagon(5 sides) has sides of (2k+0.5)units. If the perimeter of the triangle is twice the perimeter of the pentagon, find the dimensions of each shape.

Answer 1

The length of side of triangle is 5 units and length of side of pentagon is 1.5 units.

SOLUTION:

Given, An equilateral triangle has sides of length
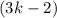`(3k-2)` units.

Then, perimeter of the triangle will be
`3 *(3 k-2)=9 k-6`

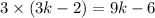
A regular pentagon (5 sides) has sides of
`(2k+0.5)` units.

Then, perimeter of the pentagon will be
`5 *(2 k+0.5)=10 k+2.5`

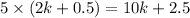
We have to find the dimensions of each shape . Now, the perimeter of the triangle is twice the perimeter of the pentagon,

So,
`\text {perimeter of triangle} = 2* \text{perimeter of pentagon}`

`\begin{array}{l}{\rightarrow 9 k-6=2(10 k+2.5)} \\\\ {\rightarrow 9 k-6=20 k+5} \\\\ {\rightarrow 20 k-9 k=-6-5} \\\\ {\rightarrow 11 k=-11} \\\\ {\rightarrow k=-1}\end{array}`

Then, length of side of triangle
`= 3(-1)-2 = - 5`

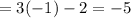
Length of side of pentagon
`= 2(-1) + 0.5 = - 1.5`

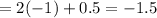
We have to neglect, negative sign as lengths can’t be negative. Even if we change the sign above all conditions are satisfied.