Question

A new automated production process averages 1.4 breakdowns per day. Because of the cost associated with a breakdown, management is concerned about the possibility of having three or more breakdowns during a day. Assume that breakdowns occur randomly, that the probability of a breakdown is the same for any two time intervals of equal length, and that breakdowns in one period are independent of breakdowns in other periods. What is the probability of having three or more breakdowns during a day?

Answer 1

The required probability is 0.167

Explanation:

Consider the provided information.

Let x be the number of breakdown per day.

A new automated production process averages 1.4 breakdowns per day.

λ=1.4

Probability of having three or more breakdowns during a day is:

`P(x\geq 3)=1-[f(0)+f(1)+f(2)]`

The Poisson probability function is:
`f(x)=(\lambda^xe^(-\lambda))/(x!)`

Therefore the required probability is:

`P(x\geq 3)=1-[(\left(1.4^(0)e^(-1.4)\right))/(0!)+(\left(1.4^(1)e^(-1.4)\right))/(1!)+(\left(1.4^(2)e^(-1.4)\right))/(2!)]`

`P(x\geq 3)\approx1-0.833`

`P(x\geq 3)=0.167`

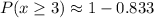
Hence, the required probability is 0.167