Question

An electron that has a velocity with x component 2.4 x 106 m/s and y component 3.6 x 106 m/s moves through a uniform magnetic field with x component 0.027 T and ycomponent -0.15 T. (a) Find the magnitude of the magnetic force on the electron. (b) Repeat your calculation for a proton having the same velocity.

I know that the equation is FB = qv × B, I'm just having difficulty computing the cross product directly? Also, I know that part b is the same answer as part a just in the opposite direction

Answer 1

(a) 7.315 x 10^(-14) N

(b) - 7.315 x 10^(-14) N

Step-by-step explanation:

As you referred at the final remark, the electron and proton undergo a magnetic force of same magnitude but opposite direction. Using the definition of magnetic force, a cross product must be done. One technique is either calculate the magnitude of the velocity and magnetic field and multiplying by sin (90°), but it is necessary to assure both vectors are perpendicular between each other ( which is not the case) or do directly the cross product dealing with a determinant (which is the most convenient approach), thus,

(a) The electron has a velocity defined as:
`\overrightarrow{v}=(2.4x10^(6) i + 3.6x10^(6) j) ([m])/([s])\\\\`

In respect to the magnetic field;
`\overrightarrow{B}=(0.027 i - 0.15 j) [T]`

The magnetic force can be written as;

`\overrightarrow{F} = q(\overrightarrow{v} x \overrightarrow{B})\\ \\\\\overrightarrow{F}= q \left[\begin{array}{ccc}i&j&k\\2.4x10^(6)&3.6x10^(6)&0\\0.027&-0.15&0\end{array}\right]`

Bear in mind
`q =-1.6021x10^(-19) [C]`

thus,

`\overrightarrow{F}= q \left[\begin{array}{ccc}i&j&k\\2.4x10^(6)&3.6x10^(6)&0\\0.027&-0.15&0\end{array}\right]\\\\\\\overrightarrow{F}= q(2.4x10^(6)* (-0.15)- (0.027*3.6x10^(6)))\\\\\\\overrightarrow{F}= -1.6021x10^(-19) [C](-457200) [T](m)/(s)\\\\\overrightarrow{F}=(7.3152x10^(-14)) k [(N*m/s)/(C*m/s)]\\\\|F|= \sqrt{ (7.3152x10^(-14))^(2)[N]^2 *k^(2)}\\\\F=7.3152x10^(-14) [N]`

Note: The cross product is operated as a determinant. Likewise, the product of the unit vector k is squared and that is operated as dot product whose value is equal to one, i.e,
`k^(2)=k\cdot k = 1`

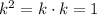
(b) Considering the proton charge has the same magnitude as electron does, but the sign is positive, thus

`\overrightarrow{F}= q \left[\begin{array}{ccc}i&j&k\\2.4x10^(6)&3.6x10^(6)&0\\0.027&-0.15&0\end{array}\right]\\\\\\\overrightarrow{F}= q(2.4x10^(6)* (-0.15)- (0.027*3.6x10^(6)))\\\\\\\overrightarrow{F}= 1.6021x10^(-19) [C](-457200) [T](m)/(s)\\\\\overrightarrow{F}=(-7.3152x10^(-14)) k [(N*m/s)/(C*m/s)]\\\\|F|= \sqrt{ (-7.3152x10^(-14))^(2)[N]^2 *k^(2)}\\\\F=-7.3152x10^(-14) [N]`

Note: The cross product is operated as a determinant. Likewise, the product of the unit vector k is squared and that is operated as dot product whose value is equal to one, i.e,
`k^(2)=k\cdot k = 1`

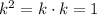
Final remarks: The cross product was performed in R3 due to the geometrical conditions of the problem.