Question

A charged particle is injected at 211 m/s into a 0.0633‑T uniform magnetic magnetic field perpendicularly to the field. The diameter of its orbit is measured and found to be 0.0389 m. What is the charge–to–mass ratio of this particle?

Answer 1

`85.68*10^3C/kg`

Step-by-step explanation:

For this problem we need the concept about Force in a Magnetic field,

For definition we know that

`F=m(v^2)/(r)`

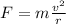
Where v is the velocity, m the mass and r the radius or distance between the two points.

We know as well that

`F = qvB`

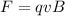
where q is the charge of a proton

v the velocity and B the magnetic field, then matching the two equation,

`qvB=m(v^2)/(r)`

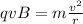
Re-arrange for q/m (charge to mass ratio)

`(q)/(m) = (v)/(Br)`

Our values are,

`v=211m/s`

`B= 0.0633T`

`r=0.0389m`

Substituting,

`(q)/(m) = (211)/(0.0633*0.0389)`

`(q)/(m) = 85689.8 C/kg = 85.68*10^3C/kg`