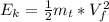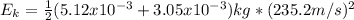Question

In an intense battle, gunfire can so concentrated that bullets from opposite sides collide in midair. Suppose that a bullet (with mass ????=5.12 g moving to the right at a speed ????=208 m/s directed 21.3∘ above the horizontal) collides and fuses with another with mass m=3.05 g moving to the left at a speed ????=282 m/s directed 15.4∘ above the horizontal.

Answer 1

velocity

a).
`v_(f)=235.2 (m/s)`

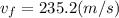
direction

b).
`\beta =71.3`

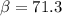
kinetic energy

c).
`E_(K)=225.97N`

Step-by-step explanation:

Those kind of question have two typical questions inside to response the final velocity and the direction finding the angle and finally the kinetic energy so each the information you need can find there so

a).

`m_(b)*v_(b)+m_(t)*v_(t)=(m_(b)+m_(t))*v_(f)`

solve to vf

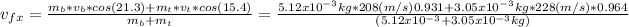
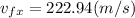
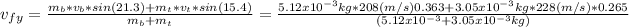
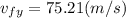
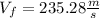
`v_(fx)=(m_(b)*v_(b)*cos(21.3)+m_(t)*v_(t)*cos(15.4))/(m_(b)+m_(t))=(5.12x10^(-3)kg*208(m/s)0.931+3.05x10^(-3)kg*228(m/s)*0.964)/((5.12x10^(-3)+3.05x10^(-3)kg))`

`v_(fx)=222.94(m/s)`

`v_(fy)=(m_(b)*v_(b)*sin(21.3)+m_(t)*v_(t)*sin(15.4))/(m_(b)+m_(t))=(5.12x10^(-3)kg*208(m/s)0.363+3.05x10^(-3)kg*228(m/s)*0.265)/((5.12x10^(-3)+3.05x10^(-3)kg))`

`v_(fy)=75.21(m/s)`

`V_(f)=\sqrt{V_(fx)^2+V_(fy)}=√(222.94^2+75.21^2)`

`V_(f)=235.28(m)/(s)`

b).

`Tan(\beta)=(v_(fx))/(v_(fy))`

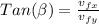
solve to β

`\beta =tan^-1*((222.94)/(75.4))`

`\beta=tan^(-1)*2.956`

`\beta =71.3`

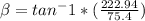
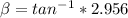
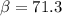
c).

Final kinetic energy

`E_(k)=(1)/(2)m_(t)*V_(f)^2`

`E_(k)=(1)/(2)(5.12x10^(-3)+3.05x10^(-3))kg*(235.2m/s)^2`

`E_(K)=225.97N`