Answer:
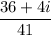
Explanation:
We are asked to find the quotient so I am assuming the question should have been:
 .
.
When we are to find
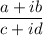 we will multiply the numerator and denominator by the conjugate of the denominator. i.e.,
we will multiply the numerator and denominator by the conjugate of the denominator. i.e.,
 .
.
Therefore,
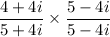
![$ ((4 + 4i)(5 - 5i))/(25 + 16) \hspace{20mm} [ Since, (a + ib)(a - ib) = a^2 + b^2] $](https://img.qammunity.org/2020/formulas/mathematics/middle-school/f52rb5yaooaedtemm8zcmyklnhziz9bf6g.png) .
.
Multiplying the numerator, we have:
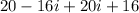 .
.
Therefore the answer is:
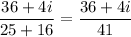 .
.
Hence, the answer.