Question

What is the zero of the function d=70-2.4t

Answer 1

Answer: The "zero" is: " 2
`(11)/(12)` " ; or, write as: " 2.92 " .

_____________________________________

→ " t = 2
`(11)/(12)` " ; or, write as: " t = 2.92 " .

_____________________________________

Explanation:

_____________________________________

Letting assume that this given function is supposed to be written as:

"distance as a function of time" ; that is:

d(t) = 70 - (2.4)t ;

→ since distance, "d" is the dependent variable (cannot be "manipulated or controlled") and as such, belongs on the "y-axis"—as the "dependent variable" ; whereas as time, "t" ; can be somewhat controlled (with respect to distance, at list as a starting point); and as such belongs on the "x-axis" as the "independent variable" .

Since no "specific units" are given to us in the problem for Either "distance" or "time" ; we shall use the term "units" to describe their values.

We have:

d(t) = 70 - (2.4)t ;

Let us rearrange this:

70 - (2.4)t ; ↔

= 70 + (- 2.4)t ; ↔

= (-2.4)t + 70 ;

And rewrite the function:

→ d(t) = (-2.4)t + 70 ;

To find the "zero" ; or "zeros" ; of this function; set "d(t)" equal to "zero" ; that is; "0" ; and solve for the value(s) for "t" when "d(t)" = 0 :

→ 0 = -2.4(t) + 70 ; ↔

Rewrite as:

→ -2.4(t) + 70 = 0 ;

For simplicity; let us multiply Each side of the equation by "10" ;

to get rid of the decimal value:

10*[ (-2.4)t) + 70 ] = 10 * [0] ;

From the left-hand side of the question:

Note the "distributive property" of multiplication:

a(b + c) = ab + ac ;

As such:

10* [-2.4(t) + 70 ] =

[10* -2.4(t)] + [10 * 70] =

-24t + 70 ;

From the "right-hand side" of the equation:

10 * 0 = 0 .

__________________________________

So; we rewrite the equation as:

-24t + 70 = 0 ;

__________________________________

Solve for " t " ;

-24t + 70 = 0 ;

Subtract "70" from Each Side of the equation;

-24t + 70 - 70 = 0 - 70 ;

to get:

-24t = -70 ;

Now, let's multiply each side of the equation by "-1" ;

to get rid of the "negative values" ;

-1* (-24t) = -1(-70) ;

to get:

24t = 70 ;

Now, let's divide Each Side of the equation by "24" ;

to isolate: "t" ; on one side of the equation; & to solve for "t" ;

24t / 24 = 70/24 ;

to get:

t = 70/24 ;

To simplify: either:

1) use calculator: 70 ÷ 24 = 2.916666666 ;

→ round to: 2.92 ;

→ t ≈ 2.92 ;

or: "
`(70)/(24) =((70/2))/((24/2))=<strong>(35)/(12)` ;

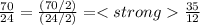→ write as simplified improper fraction: " t =
`(35)/(12)` "

→ or: write as mixed number:

→ "
`(35)/(12)` = 35 ÷ 12 =

2 R 11

12 ⟌35

- 24

1 1

→ write as: " 2
`(11)/(12)` " ;

→ " t = 2
`(11)/(12)` " .

_____________________________________

Hope this is helpful to you.

Wishing you the best!

_____________________________________