Question

The points P(2,3) , Q(-1,1) and R(5,-1) are the vertices of a triangle PQR.Find the equation of the altitude of the triangle PQR drawn from the point Q(-1,1).​

Answer 1

`y = (3)/(4) x+ (7)/(4)`

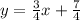
Explanation:

The slope of straight line PR where P(2,3) and R(5,-1) are two vertices of triangle PQR will be =
`(3-(-1))/(2-5) =-(4)/(3)`

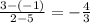
Therefore, the slope of the altitude passing through Q(-1,1) will be
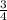`(3)/(4)` {Since, the product of slopes of two perpendicular straight line is -1}

So, equation of the altitude is
`y=(3)/(4) x + c` where c is a constant.

Now, putting x = -1 and y = 1 in the above equation we get

`1 = -(3)/(4) + c`

⇒
`c=(7)/(4)`

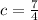
Therefore, the equation of the altitude is
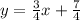`y = (3)/(4) x+ (7)/(4)` (Answer)