Answer:
Diverge
Explanation:
(a)
1st year:
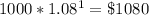
2nd year:

3rd year:
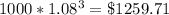
4th year:
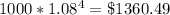
5th year:
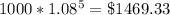
(b) The sequence is divergent, because if we take the derivative of the function with respect to n year:
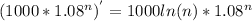
This is a positive, meaning the slope of the function is positive. If we take the second derivative using product rule
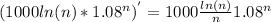
This is also positive when n > 0. Therefore, the slope is positive and increasing. This means the sequence diverges.