Question

Assume that the heights of women are normally distributed with a mean of 63.6 inches and a standard deviation of 2.5 inches. If 100 women are randomly selected, find the probability that they have a mean height greater than 63.0 inches.

Answer 1

58%

Explanation:

Answer 2

The probability is 58 %.

Explanation:

This problem belong to a normal distribution probability.

Mean = 63.6

Standard Deviation = 2.5.

We have to find the probability of a height greater than 63.0.

Due to the normal probability, we need to find the Z score first:

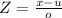`Z=(x-u)/(o)`; where x is the height, u is the mean, and o is the standard deviation.

`Z=(63-63.6)/(2.5) \\Z= -0.24`

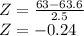
Once we have our Z score, we find the probability with the z-table (attached). So, for a z score of -0.24 we have a probability of 0.42.

But, the problem is asking for height greater than 63.0, this mean that we have to subtract 0.42 from 1, giving as result 0.58, which means a 58% of probability,