Answer:
It would take 2 second to reach its maximum height.
The maximum height of the ball is 43.6 meters above the ground.
Explanation:
Consider the provided function.
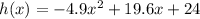
The above function's graph is a downward parabola and the maximum of the downward parabola is at its vertex.
We can find the x coordinate of the function using the formula:

Substitute a=-4.9 and b=19.6 in


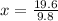
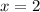
Hence, it would take 2 second to reach its maximum height.
Substitute x=2 in above formula.

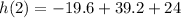

Hence, the maximum height of the ball is 43.6 meters above the ground.