Answer:
Part a) We should try to eliminate the y's because the coefficients are the same
Part b) The solution is the point (6,-9)
Explanation:
Part a) Which variable pair should we try to eliminate?
we have
 ----> equation 1
----> equation 1
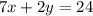 ----> equation 2
----> equation 2
Solve by elimination
We should try to eliminate the y's because the coefficients are the same
Part b) What is the solution to the system?
Multiply equation 2 by -1 both sides
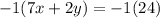
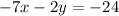 -----> equation 3
-----> equation 3
Adds equation 1 and equation 3
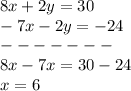
Find the value of y
![8x+2y=30[/tex</p><p>[tex]8(6)+2y=30](https://img.qammunity.org/2020/formulas/mathematics/middle-school/71ky0nbr3ldv0ph6maqie44bwyavf8x3j3.png)
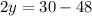
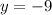
The solution is the point (6,-9)