Question

Given a circle with measures of (C, d, and r) and a circle with measures of (C' ,d' , and r'). what is C' if d/d'=.25 and C=6?​

Answer 1

The value of c' is 24

Explanation:

Given as for circle :

C = 6 And
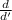`(d)/(d')` = .25

For circle first

The Circumference of circle = C

Diameter of circle = d

Radius of circle = r

So , circumference of circle = 2
`\pi` r

For circle second

The Circumference of circle = C'

Diameter of circle = d'

Radius of circle = r'

So , circumference of circle = 2
`\pi` r'

Now,
`(c)/(c')` =
`(2 \pi  r)/(2 \pi  r')`

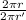
Or, ∵ Diameter = 2 × Radius

So,
`(c)/(c')` =
`(2 \pi  d)/(2 \pi  d')`

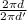
Or,
`(6)/(c')` =
`(2 \pi  d)/(2 \pi  d')`

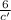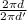
So,
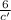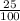
`(6)/(c')` =
`(25)/(100)`

∴ c' =
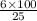`(6* 100)/(25)` = 24

Hence The value of c' is 24 Answer