Question

At 10:30 AM, detectives discover a dead body in a room and measure its temperature at 31∘C. One hour later, the body’s temperature had dropped to 24.8∘C. Determine how many hours had passed since the death occured (when the body temperature was a normal 37∘C), by the time the body was discovered, assuming that the temperature in the room was held constant at 20∘C. (Use decimal notation. Give your answer to one decimal place. Round any intermediate calculations, if needed, to no less than three decimal places.)

Answer 1

The reference time is 10:30 AM,

The body temperature is 31 ° C,

The room temperature (
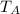`T_A`) is 20 ° c,

Newton and the law of cooling are useful in this situation, the equation says,

`(dT)/(dt) = -k(T-T_A)`

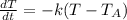
Where k is proportionality constant

t= time

T= Temperature of Body,

Thus,

`(dT)/(dt) = - k(T-20)`

`(1)/(T-20)dT = -kdt`

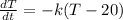
We can integrate here,

`\int (1)/(T-20)dT = -k\int dt`

`ln(T-20) = -kt+c`

`T-20=e^(-kt+c)`

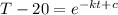
We have our first equation,

`T=20+e^(-kt)e^c`

When the measurement t = 0 was made, the temperature T = 31 ° c

`31=20+e^(-k(0))e^c`

11=e^c

We have know that
`e^c = 11`

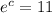
Our equation now is,

`T=20+11e^(-kt)`

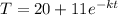
When t=1hour then T=24.8, then

`24.8=20+11e^(-k(1))`

`24.8-20=11e^(-k)`

`(4.8)/(11)=e^(-k)`

`ln((4.8)/(11))=-k`

`-k=-0.83`

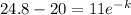
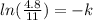
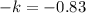
Then our equation is now,

`T=20+11e^(0.83t)`

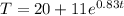
Finally, we know can find the time when T=37, so

`37=20+11e^(-0.83t)`

`e^(-0.83t)=(17)/(11)`

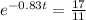
-0.83t=ln\frac({17}{11})

`t=-0.52`

`t=31min`

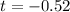
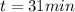
Therefore the time is 10:30-31min, we have that at 9:59AM the body was still alive