Question

A slender rod is 80.0 cm long and has mass 0.370 kg . A small 0.0200-kg sphere is welded to one end of the rod, and a small 0.0500-kg sphere is welded to the other end. The rod, pivoting about a stationary, frictionless axis at its center, is held horizontal and released from rest. What is the linear speed of the 0.0500 kg sphere as it passes through its lowest point?

Answer 1

1.10 m/s

Step-by-step explanation:

Linear speed is given by

`v=r\omega`

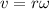
Kinetic energy is given by

`KE=0.5I\omega^(2)`

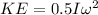
Potential energy

PE= mgh

From the law of conservation of energy, KE=PE hence

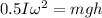`0.5I\omega^(2)=mgh` where m is mass, I is moment of inertia,
`\omega` is angular velocity, g is acceleration due to gravity and h is height

Substituting m2-m1 for m and 0.5l for h,
`\frac {2v}{L}` for
`\omega` we obtain

`0.5I(\frac {2v}{L})^(2)=0.5Lg(m2-m1)`

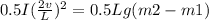
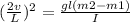`(\frac {2v}{L})^(2)=\frac {gl(m2-m1)}{I}` and making v the subject

`v^(2)=\frac {gl^(3)(m2-m1)}{4I}`

`v=\sqrt {\frac {gl^(3)(m2-m1)}{4I}}`

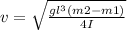
For the rod, moment of inertia
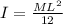`I=\frac {ML^(2)}{12}` and for sphere
`I=MR^(2)` hence substituting 0.5L for R then
`I=M(0.5L)^(2)`

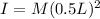
For the sphere on the left hand side, moment of inertia I

`I=m1(0.5L)^(2)` while for the sphere on right hand side,
`I=m2(0.5L)^(2)`

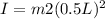
The total moment of inertia is therefore given by adding

`I=\frac {ML^(2)}{12}+ m1(0.5L)^(2)+ m2(0.5L)^(2)=\frac {L^(2)(M+3m1+3m2)}{12}`

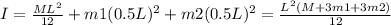
Substituting
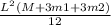`\frac {L^(2)(M+3m1+3m2)}{12}` for I in the equation
`v=\sqrt {\frac {gL^(3)(m2-m1)}{4I}}`

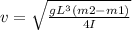
Then we obtain

`v=\sqrt {\frac {gL^(3)(m2-m1)}{4(\frac {L^(2)(M+3m1+3m2)}{12})}}=\sqrt {\frac {3gL^(3)(m2-m1)}{L^(2)(M+3m1+3m2)}}`

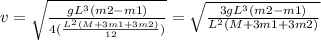
This is the expression of linear speed. Substituting values given we get

`v=\sqrt {\frac {3*9.81*0.8^(3)(0.05-0.02)}{0.8^(2)(0.39+3(0.02)+3(0.05))}} \approx 1.08 m/s`