Question

The given line passes through the points (0, -3) and (2, 3).

What is the equation, in point-slope form of the line that is
parallel to the given line and passes through the point
(-1, -1)?
y+1 = - 3(x + 1)
+1 = -(x + 1)
v+1 = $(x + 1)
5
-3 -2 1
/1
3
4
y + 1 = 3(x + 1)
Save and Exit
Mark this and return

Answer 1

The equation, in point-slope form of the line that is parallel to the given line and passes through the point (-1, -1) is y + 1 = 3(x + 1).

Solution:

Given that, a line passes through (0, -3) and (2, 3).

We have to find the line equation which is parallel to above line and passes through (-1, -1).

Now, let us find the slope of the given line.

`\text { slope } m=(y_(2)-y_(1))/(x_(2)-x_(1)), \text { where }\left(x_(1), y_(1)\right) \text { and }\left(x_(2), y_(2)\right) \text { are points on that line }`

`\text { Then, } m=(3-(-3))/(2-0)=(3+3)/(2)=(6)/(2)=3`

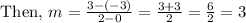
So, slope of given line is 3,

Then, slope of required line is also 3, as slopes of parallel lines are equal.

Then, required line equation in point – slope form is given as:

`\begin{array}{l}{y-y_(1)=m\left(x-x_(1)\right)} \\\\ {y-(-1)=3(x-(-1))} \\\\ {\rightarrow y+1=3(x+1)}\end{array}`

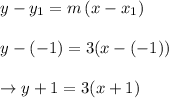
Hence, the line equation is y + 1 = 3(x + 1).