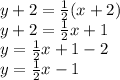Question

What is the equation, in slope-intercept form, of the line that is perpendicular to the line

y - 4 = -2(x - 6) and passes through the point (-2,-2)?
O y=-x - 10
O y= {x + 10
O y=zx-1
O y=2x +1
Mark this and return
Save and Exit
Next

Answer 1

`y=(1)/(2) x-1`

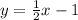
Explanation:

The initial line is given in "point-slope form" (
`y-y_0=m(x-x_0)` therefore we can easily extract from it the slope, and obtain from it what should be the slope of a line perpendicular to it:

Given the expression:
`y-4=-2(x-6)`

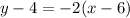
we understand that the slope is "-2", and the point through which the line passes is the point (6,4) on the plane. We are concerned about the slope, since a line perpendicular to the given line must have a slope that corresponds to the "opposite of the reciprocal" of the original slope.

The opposite of "-2" is "2", and the reciprocal of this is "1/2".

Therefore the slope of the perpendicular line must be "1/2".

Now we can build the equation of the line perpendicular line through the point (-2,-2) by using again the "point-slope form":

`y-y_0=m(x-x_0)\\y-(-2)=(1)/(2) (x-(-2))\\y+2=(1)/(2) (x+2)`

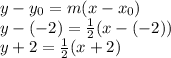
Solving for y in this last expression we express the line in slope_y-intercept form:

`y+2=(1)/(2) (x+2)\\y+2=(1)/(2) x+1\\y=(1)/(2) x+1-2\\y=(1)/(2) x-1`