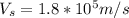Question

A spaceship, at rest in some inertial frame in space, suddenly needs to accelerate. The ship forcibly expels 103 kg of fuel from its rocket engine, almost instantaneously, at velocity (3IS)c in the original inertial frame; afterwards the ship has a mass of 106 kg. How fast will the ship then be moving, valid to three significant figures?

Answer 1

`V_s = 1.8*10^5m/s`

Step-by-step explanation:

There is no external force applied, therefore there is a moment's preservation throughout the trajectory.

Initial momentum = Final momentum.

The total mass is equal to

`m_T= m_1 +m_2`

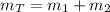
Where,

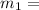`m_1 =` mass of ship

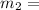`m_2 =` mass of fuell expeled.

As the moment is conserved we have,

`0=V_fm_2+V_sm_1`

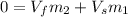
Where,

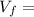`V_f =` Velocity of fuel

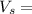`V_s =`Velocity of Space Ship

Solving and re-arrange to
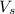`V_s`we have,

`V_s = (V_f m_2 )/(m_1)`

`V_s = (3/5c)/(10^6)`

`V_s = 3.5*10^(-3)c`

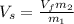
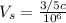
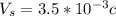
Where c is the speed of light.

Therefore the ship be moving with speed

`V_s = (3)/(5)*10^(-3)*3*10^8m/s`

`V_s = 1.8*10^5m/s`