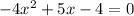Question

-4x^2+5x-4=0 what are the real solutions

Answer 1

`-4 x^(2)+5 x-4=0` will not have real roots that means quadratic equation do not have real solution.

Solution:

Need to determine the real solutions for following quadratic equations

`-4 x^(2)+5 x-4=0`

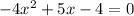
First let’s check whether the given quadratic equation have real roots or not

`\begin{array}{l}{\text { General quadratic equation } a x^(2)+b x+c=0 \text { will have real roots only }} \\ {\text { when } b^(2)-4 a c>0}\end{array}`

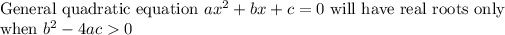
In our case, equation is
`-4 x^(2)+5 x-4=0`

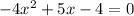
Here a = -4, b = 5 and c = -4

Substituting the values in
`b^(2)-4 a c`

`\begin{array}{l}{\Rightarrow \mathrm{b}^(2)-4 \mathrm{ac}=5^(2)-4 *(-4) *(-4) } \\\\ {=25-64=-39}\end{array}`

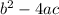
So since in our case
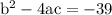`\mathrm{b}^(2)-4 \mathrm{ac}=-39` which is not greater than zero, so quadratic equation
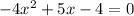`-4 x^(2)+5 x-4=0` will not have real roots that means quadratic equation do not have real solution.