Question

A fourth-order polynomial passes through the five points for which the independent and dependent variables, x and y, respectively, are given as (−2, 37), (−1, 7), (0, 5), (1, 13), and (2, 61). Find the polynomial by any suitable method. Here, x represents the spatial location and y the species concentration in a chemical reactor.

Answer 1

The fourth-order polynomial that passes through the points is
`P(x)=2x^4+x^3+3x^2+2x+5`

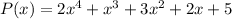
Explanation:

A fourth-order polynomial has this general form:

`P(x)=ax^4+bx^3+cx^2+dx+e`

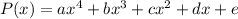
We need to replace the given points one by one, which leads to a system of 5 equations and 5 variables (namely a,b,c,d,e)

`37=a(-2)^4+b(-2)^3+c(-2)^2+d(-2)+e\\7=a(-1)^4+b(-1)^3+c(-1)^2+d(-1)+e\\5=a(0)^4+b(0)^3+c(0)^2+d(0)+e\\13=a(1)^4+b(1)^3+c(1)^2+d(1)+e\\61=a(2)^4+b(2)^3+c(2)^2+d(2)+e`

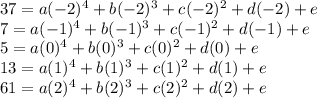
We can rewrite this system as follows:

`16a-8b+4c-2d+e=37\\a-b+c-d+e=7\\e=5\\a+b+c+d+e=13\\16a+8b+4c+2d+e=61`

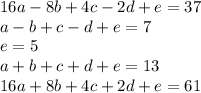
We can use the Gaussian Elimination to solve this system of equations. To use the Gaussian Elimination we need to express the system of linear equations in matrix form (the matrix equation Ax = b).

The coefficient matrix (A) for the above system is

`\left[\begin{array}{ccccc}16&-8&4&-2&1\\1&-1&1&-1&1\\0&0&0&0&1\\1&1&1&1&1\\16&8&4&2&1\end{array}\right]`

the variable matrix (x) is

`\left[\begin{array}{c}a&b&c&d&e\end{array}\right]`

and the constant matrix (b) is

`\left[\begin{array}{c}37&7&5&13&61\end{array}\right]`

The augmented matrix for this system, it is obtained by appending the columns of the coefficient matrix and the constant matrix.

`\left[\begin{array}c16&-8&4&-2&1&37\\1&-1&1&-1&1&7\\0&0&0&0&1&5\\1&1&1&1&1&13\\16&8&4&2&1&61\end{array}\right]`

The augmented matrix can be transformed by a sequence of elementary row operations to the reduced row echelon form.

`\left[\begin{array}ccccc1&0&0&0&0&2\\0&1&0&0&0&1\\0&0&1&0&0&3\\0&0&0&1&0&2\\0&0&0&0&1&5\end{array}\right]`

Therefore the solutions are:

`\left\begin{array}{c}a=2&b=1&c=3&d=2&e=5\end{array}\right`

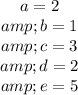
And the polynomial P(x) is:

`P(x)=2x^4+x^3+3x^2+2x+5`

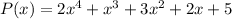
We can check our solution plotting the polynomial and checking that it passes through the points.