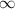Question

F(x) = 5-4x-x^2
find
a) the interval on which f is increasing and decreasing

Answer 1

*Answers represent ranges not coordinates*

Increasing on
`(-{\infty},-2)`

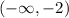
Decreasing on
`(2,{\infty})`

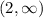
Explanation:

Graphical Approach:

If we graph
`f(x)` we get the graph of the attached image. Reading the function from left to right we can see that the function goes up until it reaches x=-2. Then it proceeds to decrease or in other words become negative. This means that it t is increasing from
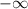`-\infty` to -2 and is decreasing from -2 to
`\infty`.

Calculus Approach:

To do this we must first take the first derivative of the function. Taking the first derivative gives us:

`f'(x)=-2x-4`

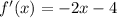
We then set the function equal to zero. This is because any extrema (minimums or maximums) of the original function become zeroes in the derivative. This is helpful as at extrema the function switches from increasing to decreasing or vice versa. Another important part is that when the first derivative is negative (the y values are negative) the original is decreasing. When the first derivative is positive (the y values are positive) the original is decreasing.

So, setting
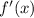`f'(x)` to zero we get:

`-2x-4=0\\-2x=4\\x=-2`

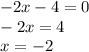
By plugging in neighboring values around x=-2 into the derivative, we can see that x values before x=-2 are positive and that the x values after x=-2 are negative. This means that the original function is increasing until it hits x=-2 and then decreases (aka its a max).

Therefore it is increasing from
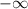`-\infty` to -2 and is decreasing from -2 to
`\infty`