Question

The sides of a square all have a side length of y. Write a simplified area function in terms of y for a rectangle whose length is twice the side length of the square and whose width is 2 units longer than the side length of the square

Answer 1

The simplified area function for the rectangle in terms of side length y of a square is 2y^2 + 4y, where the rectangle's length is twice the side length of the square and the width is 2 units longer.

Step-by-step explanation:

The student is asked to write a simplified area function for a rectangle in terms of the variable y, where the length of the rectangle is twice the side length of a square and the width is 2 units longer than the side of the square. Given that the side of the square is y, the length of the rectangle would be 2y and the width would be y+2. To find the area of the rectangle, you multiply the length by the width:

Area of rectangle = Length × Width

= 2y × (y+2)

= 2y^2 + 4y

Thus, the simplified area function of the rectangle in terms of y is 2y^2 + 4y.

Answer 2

The simplified area function in terms of y for a rectangle is
`f(y)=2 y^(2)+4 y`

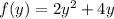
Solution:

Given that length of each side of a square = y

Need to determine area of rectangle whose length is twice the length of the square and width is 2 units longer that the side length of square

Length of rectangle = twice of side length of square =
`2 * y = 2y`

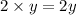
Width of rectangle = 2 + side length of square = 2 + y = y + 2

`\text { Area of rectangle }=\text { length of rectangle } * \text { width of rectangle.}`

On substituting length and width in formula for area, we get

`\text { Area of rectangle }=2 y * (y+2)=2 y^(2)+4 y`

Hence function
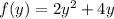`f(y)=2 y^(2)+4 y` is represents area of required rectangle.