Answer :
(a) The value of
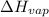 is 48.6 kJ/mol
is 48.6 kJ/mol
(b) The the normal boiling point is 489.2 K
(c) The entropy of vaporization at the boiling point is 99.3 J/K
Explanation :
(a) To calculate
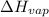 of the reaction, we use clausius claypron equation, which is:
of the reaction, we use clausius claypron equation, which is:
![\ln((P_2)/(P_1))=(\Delta H_(vap))/(R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/4vtbgz8qequ3vvsclhkmmvxlsikmj2gcnu.png)
where,
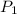 = vapor pressure at temperature
= vapor pressure at temperature
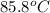 = 1.3 kPa
= 1.3 kPa
 = vapor pressure at temperature
= vapor pressure at temperature
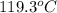 = 5.3 kPa
= 5.3 kPa
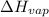 = Enthalpy of vaporization = ?
= Enthalpy of vaporization = ?
R = Gas constant = 8.314 J/mol K
 = initial temperature =
= initial temperature =
![85.8^oC=[85.8+273]K=358.8K](https://img.qammunity.org/2020/formulas/physics/college/laynu7da2g8vq6nv5nhoy6okzbz5ektuzx.png)
 = final temperature =
= final temperature =
![119.3^oC=[119.3+273]K=392.3K](https://img.qammunity.org/2020/formulas/physics/college/h7a736x0pyekdo8tl68gumi62mxkxcqlkb.png)
Putting values in above equation, we get:
![\ln((5.3kPa)/(1.3kPa))=(\Delta H_(vap))/(8.314J/mol.K)[(1)/(358.5)-(1)/(392.3)]\\\\\Delta H_(vap)=48616.4J/mol=48.6kJ/mol](https://img.qammunity.org/2020/formulas/physics/college/71c6vh1ex4aw91yg5roaylxskhtlqyhtdx.png)
Therefore, the value of
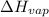 is 48.6 kJ/mol
is 48.6 kJ/mol
(b) The clausius claypron equation is:
![\ln((P_2)/(P_1))=(\Delta H_(vap))/(R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/4vtbgz8qequ3vvsclhkmmvxlsikmj2gcnu.png)
where,
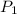 = vapor pressure at temperature
= vapor pressure at temperature
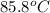 = 1.3 kPa
= 1.3 kPa
 = vapor pressure at temperature normal boiling point = 101.3 kPa
= vapor pressure at temperature normal boiling point = 101.3 kPa
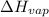 = Enthalpy of vaporization = 48.6 kJ/mol
= Enthalpy of vaporization = 48.6 kJ/mol
R = Gas constant =
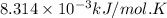
 = initial temperature =
= initial temperature =
![85.8^oC=[85.8+273]K=358.8K](https://img.qammunity.org/2020/formulas/physics/college/laynu7da2g8vq6nv5nhoy6okzbz5ektuzx.png)
 = final temperature = ?
= final temperature = ?
Putting values in above equation, we get:
![\ln((101.3kPa)/(1.3kPa))=(48.6kJ/mol)/(8.314* 10^(-3)kJ/mol.K)[(1)/(358.5)-(1)/(T_2)]\\\\T_2=489.2K](https://img.qammunity.org/2020/formulas/physics/college/d3rvn8pb8xtsiwah6r3twpeqx7v5xhso4h.png)
Therefore, the normal boiling point is 489.2 K
(c) Now we have to determine the entropy of vaporization at the boiling point.
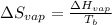
where,
 = entropy of vaporization = ?
= entropy of vaporization = ?
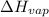 = enthalpy of vaporization = 48.6 kJ/mol
= enthalpy of vaporization = 48.6 kJ/mol
 = boiling point = 489.2 K
= boiling point = 489.2 K
Now put all the given values in the above formula, we get:
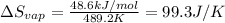
Therefore, the entropy of vaporization at the boiling point is 99.3 J/K