Question

The standard IQ test is designed so that the mean is 100100 and the standard deviation is 1515 for the population of all adults. We wish to find the sample size necessary to estimate the mean IQ score of statistics students. Suppose we want to be 9090% confident that our sample mean is within 22 IQ points of the true mean. Assume then that σ=15σ=15 and determine the required sample size.

Answer 1

The sample size should be approximately 151.

Explanation:

We are given the following in the question:

Population mean, μ = 100

Population standard deviation, σ = 15

We have to evaluate the sample size, n.

Alpha, α = 0.10

Confidence interval:

`\mu \pm z_(critical)(\sigma)/(√(n))`

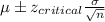
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.10) = \pm 1.64`

`100 \pm 1.64((15)/(√(n)) ) = (98,102)`

`100 \pm 1.64(\displaystyle(15)/(√(n)) ) = (98,102)\\\\1.64((15)/(√(n)) ) = 2\\\\n = 151.29 \approx 151`

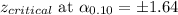
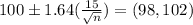
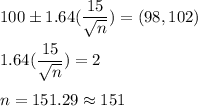
Thus, the sample size should be approximately 151.