Question

Aki's Bicycle Design has determined that when x hundred bicycles are built, the average cost per bicycle =0.9x^2-1.7x+10.861, when C(x) is in hundreds of dollars. How many bicycles should the shop build to minimize the average cost per bicycle?

C(x)=0.9x^2-1.7x+10.861 =
C(x)=0.9(x^2-1.889x)+10.861=
My question is how do they come up with the 1.889 in the equation?

Answer 1

About 89 bicycles.

Explanation:

Let C(x) is average cost (in hundreds of dollars) per bicycle and x be the number bicycles built (in hundred).

`C(x)=0.9x^2-1.7x+10.861`

We need to find the number of bicycles for which the average cost per bicycle is minimum.

The vertex form of a parabola is

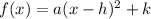`f(x)=a(x-h)^2+k` .... (1)

where, a is constant and (h,k) is vertex.

`C(x)=(0.9x^2-1.7x)+10.861`

Taking out 0.9 from the parenthesis.

`C(x)=0.9(x^2-1.889x)+10.861`

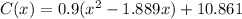
If an expression is
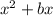`x^2+bx`, then we add
`((b)/(2))^2` in the expression to make it perfect square.

Here, b=-1.889,

`((b)/(2))^2=((-1.889)/(2))^2=0.892`

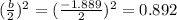
Add an d subtract 0.892 in the parenthesis.

`C(x)=0.9(x^2-1.889x+0.892-0.892)+10.861`

`C(x)=0.9(x^2-1.889x+0.892)+0.9(-0.892)+10.861`

`C(x)=0.9(x^2-0.892)^2-0.8028+10.861`

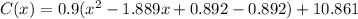
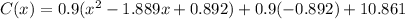
`C(x)=0.9(x^2-0.892)^2+10.0582` ... (2)

From (1) and (2) we get

`h=0.892,k=10.0582`

Aki should built 0.892 hundred bicycle to minimize the average cost per bicycle.

`0.892* 100=89.2\approx 89`

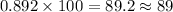
Therefore, the Aki should built 89 bicycle to minimize the average cost per bicycle.