Question

A government official is in charge of allocating social programs throughout the city of Vancouver. He will decide where these social outreach programs should be located based on the percentage of residents living below the poverty line in each region of the city. He takes a simple random sample of 123 people living in Gastown and finds that 25 have an annual income that is below the poverty line.

Use the sample data to compute a 95% confidence interval for the true proportion of Gastown residents living below the poverty line.

(Please carry answers to at least six decimal places in intermediate steps.)

95% confidence interval = ( )

Answer 1

A 95% confidence interval for the true proportion of Gastown residents living below the poverty line is (0.1321, 0.2744).

In Mathematics and Statistics, the sample proportion of a sample can be calculated by using this formula:

`\hat{p} = (x)/(n)`

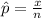
Where:

• x represent the total number of individuals that are having a specified characteristic.
• n represent the total number of individuals that are in the sample.

By substituting the given parameters, we have the following:

Sample proportion,
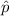`\hat{p}` = 25/123

Sample proportion,
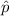`\hat{p}` = 0.203252

For a confidence level of 95%, the critical value of z is given by;

Critical value, z* = 1.960

Now, we can calculate the confidence interval (CI) by using the following formula;

`CI=\hat{p}\pm z^(*)\sqrt{\frac{\hat{p}(1-\hat{p})}{n} } \\\\CI=0.203252 \pm 1.960 \sqrt{(0.203252(1-0.203252))/(123) } \\\\CI=0.203252 \pm 1.960 \sqrt{(0.161941)/(123) }`

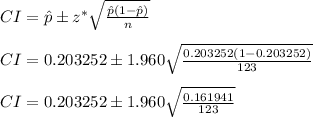
CI = (0.203252 ± 1.960(0.036285))

CI = (0.203252 ± 0.0711186)

CI = (0.203252 - 0.0711186, 0.203252 + 0.0711186)

CI = (0.1321, 0.2744)

Answer 2

Answer: (0.132132, 0.274368)

Explanation:

Given : A simple random sample of 123 people living in Gastown and finds that 25 have an annual income that is below the poverty line.

i.e. n= 123

`\hat{p}=(25)/(123)\approx0.203252`

Critical value for 95% confidence interval :
`z_(\alpha/2)=1.96`

Confidence interval for population :

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

i.e.
`0.203252\pm (1.96)\sqrt{(0.203252(1-0.203252))/(123)}`

`0.203252\pm (1.96)\sqrt{(0.203252(1-0.203252))/(123)}\\\\\0.203252\pm0.071118\\\\=(0.20325-0.071118,\ 0.203252+0.071118)\\\\=(0.132132,\ 0.274368)`

Hence, the 95% confidence interval for the true proportion of Gastown residents living below the poverty line : (0.132132, 0.274368)