Question

In equilateral ∆ABC, points M, P, and K belong to AB , BC , and AC respectively and AM:MB = BP:PC = CK:KA = 1:3. Prove that ∆MPK is an equilateral triangle.

Answer 1

See explanation

Explanation:

In equilateral ∆ABC,

`AB = BC = AC=a`

`m\angle A=m\angle B=m\angle C=60^(\circ)`

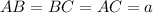
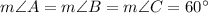
Points M, P, and K belong to AB , BC , and AC respectively and

AM:MB = BP:PC = CK:KA = 1:3.

So,

`AM = BP = CK =(1)/(4)a`

`MB = PC = KA =(3)/(4)a`

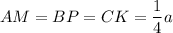
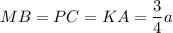
Triangles AMK, BPM and CKP are all congruent by SAS postulate, so

`MK=MP=PK`

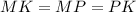
If
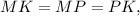`MK=MP=PK,` triangle MPK is equilateral triangle