Question

A college financial adviser is interested in studying the number of students at his college who apply for loans when entering graduate school. Of the 721 students at the college, 299 of them apply for loans when entering graduate school. If the financial adviser conducts a study and samples 45 students at the college who are starting graduate school next fall, what is the probability that more than 16 of them apply for loans?

Answer 1

0.7429

Explanation:

Given that Of the 721 students at the college, 299 of them apply for loans when entering graduate school.

So p = proportion of students applying for loans =
`(299)/(721) =0.415`

Each student is independent of the other and there are two outcomes

Hence out of 45 students the no of students who apply for loans say X is binomial with n =45 and p = 0.415

the probability that more than 16 of them apply for loans

=
`P(X>16)\\= \Sigma_(x=17) ^(45)  P(x)\\=\Sigma_(x=17) ^(45)(45Cx (0.415)^x (0.585)^(25-x) )`

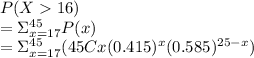
=0.7429