Question

1. The pressure is an automobile tire depends on the temperature of the air in the tire. For a specific tire, the air temperature is initially 25oC, and the pressure gage reads 210 kPa. The tire is then driven on the freeway for two hours, and the air temperature in the tire rises to 50oC. If the volume of the tire is 0.025 m3 and the atmospheric pressure is 100 kPa a. Determine the mass of the air in the tire, in kg. b. Find the final pressure of the air in the tire, in kPa. c. Calculate the heat transfer during this process, in kJ. d. What is the source of the heat transfer?

Answer 1

a) m = 90.39 10-3 kg , b) P2 = 336 kPa , c) Q = 0.1465 kJ and d)

friction force

Step-by-step explanation:

The air behaves in the first approximation as an ideal gas so we will use the ideal gas equation

P V = n R T

Where P, V and T are the pressure, volume and absolute temperature (Kelvin), n is the number of moles and R is the gas constant with a value of 8.314 J / mol K

a) Let's calculate the number of moles of gas

T = 273 +25 = 298K

P = 100 103 + 210 103 = 310 103 Pa

n = PV / RT

n = 310 103 0.025 / (8.314 298)

n = 3.12 mol

The air is mainly composed of two gases 78% nitrogen and oxygen 21, the Tor 1% are several gases (CO2, water vapor, etc.), we will neglect this 1%.

Atomic weights oxygen = 16 g / mol

Atomic weight Nitrogen = 14 g / mol

The molecule of each gas is formed by two atoms, so the molecular weights (PM) are

Oxygen PM = 2 16 = 32 g / mol

PM nitrogen = 2 14 = 28 g / mol

Molecular weight of air is

Pm air = 32 0.21 + 28 0.78 = 28.56 g / mol

The molecular weight value of the tables is 28.97 g/mol, for the calculation we will use this value

Now let's use the definition of mol

n = m / PM

m = PM n

m = 28.97 3.12

m = 90.39 g

m = 90.39 10-3 kg

b) To find the final pressure, write the equation of the ideal gases for the two points

P1 V = n R T1

P2 V = n R T2

Resolve and calculators

T1 = 298K

T2 = 273 +50 = 323K

P1 / P2 = T1 / T2

P2 = p1 T2 / T1

P2 = 310 103 323/298

P2 = 336 103 Pa

P2 = 336 kPa

c) The heat transferred

Q = m
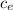`c_(e)` ΔT = m
`c_(e)` (
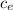`T_(f)`-T₀)

We need to find the specific heat of the air, let's use redefined specific heat that is derived from the energy with respect to the constant volume temperature. Energy

U = 5/2 NKT = 5/2 nRT

Where 5 comes from the fact that the molecule is diatomic, for monatomic molecular 3

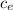`c_(e)` = (dU/dT) v = 5/2 nR

We replace we calculate

Q = m 5/2 nR (
`T_(f)`-T₀)

Q = 5/2 90.39 3.12 8.314 (323-298)

Q = 146.5 J

Q = 0.1465 kJ

d) the source of this heat is between the tires and the pavement,

friction force