Question

Suppose you know that Mr. and Mrs. Vincent have at most eight children. One day you happen to meet two girls who were the Vincent children. When you told the Vincents about this they told you that the chance of this happening is exactly 1/2, i.e., the probability that two of the Vincent children, randomly chosen, are both girls is exactly 1/2. How many children do the Vincent’s have, exactly? Of them what is the exact number of girls?

Answer 1

The number of children are 4 out of which 3 are girls

Explanation:

Data provided in the question:

P(Two randomly selected children are girls) =
`(1)/(2)`

now,

let the number of children be 'n'

the number of girls be 'x'

thus,

P(Two randomly selected children are girls) =
`(^xC_2)/(^nC_2)` =
`(1)/(2)`

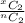also,

`^nC_r` =
`(n!r!)/((n-r)!)`

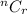thus,

`((x!2!)/((x-2)!))/((n!2!)/((n-2)!))` =
`(1)/(2)`

or

`(x(x-1))/(n(n-1))`=
`(1)/(2)`

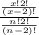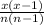or

2x(x-1) = n(n-1)

now

for x = 3 and n = 4

i.e

2(3)(3-1) = 4(4-1)

12 = 12

hence, the relation is justified

therefore,

The number of children are 4 out of which 3 are girls