Question

The Cubs and Blue Jays play in the World Series where the first team to win 4 games is declared the overall winner. Suppose that the Cubs are stronger than the Blue Jays, and the Cubs win each game with probability 0.6, independently of the outcomes of the other games.

a.Find the probability, for i = 4, 5, 6, 7, That the cubs win the World Series in exactly i games.

b.What is the probability that the Cubs would win in a 2-out-of-3 series instead ?

Answer 1

a)

There is a 12.96% probability that the Cubs win the World Series in exactly four games.

There is a 20.736% probability that the Cubs win in 5 games.

There is a 20.736% probability that the Cubs win in 6 games.

There is a 16.60% probability that the Cubs win in 7 games.

b)

There is a 64.8% probability that the Cubs would win in a 2-out-of-3 series.

Explanation:

For each game, there are these following probabilities:

A 60% probability that the Cubs win.

A 40% probability that the Blue Jays win.

The combination formula is important to solve this problem:

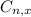`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

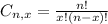
a.Find the probability, for i = 4, 5, 6, 7, That the cubs win the World Series in exactly i games.

i = 4.

This is the probability that the Cubs win in 4 games. So

`P = (0.6)^(4) = 0.1296`

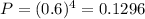
There is a 12.96% probability that the Cubs win the World Series in exactly four games.

i = 5.

This is the Cubs winning four games and the Blue Jays 1. The Blue Jays win cannot happen in the fifth game, so the number of possibilities is a combination of 4 by 3. So

`C_(4,,3) = (4!)/(3!(4-3)!) = 4`

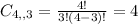
The probability that the Cubs win in 5 games is:

`P = 4*(0.6)^4*(0.4) = 0.20736`

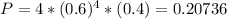
There is a 20.736% probability that the Cubs win in 5 games.

i = 6.

This is the Cubs winning four games and the Blue Jays 2. The Blue Jays cannot win game 6, so the number of possibilities is a combination of 5 by 3.

`C_(5,3) = (5!)/(3!(5-3)!) = 10`

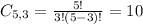
The probability that the Cubs win in 6 games is:

`P = 10*(0.6)^4*(0.4)^2 = 0.20736`

There is a 20.736% probability that the Cubs win in 6 games.

i = 7.

This is the Cubs winning four games and the Blue Jays 3. The Blue Jays cannot win game 7, so the number of possibilities is a combinaiton of 6 by 3.

`C_(6,3) = (6!)/(3!(5-3)!) = 20`

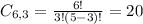
The probability that the Cubs win in 7 games is:

`P = 20*(0.6)^4*(0.4)^3 = 0.1660`

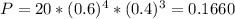
There is a 16.60% probability that the Cubs win in 7 games.

b.What is the probability that the Cubs would win in a 2-out-of-3 series instead ?

This is the sum of the probabilities that they win in 2 games and the they win in 3 games.

i = 2.

This is the Cubs winning both games. So

`P_(1) = 0.6*0.6 = 0.36`

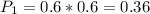
i = 3.

This is the Cubs winning 2 games and the Blue Jays 1. The Blue Jays cannot win game 3. So the number of possibilities is a combination of 2 by 1.

`C_(2,1) = (2!)/(1!(2-1)!) = 2`

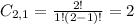
And the probability is:

`P_(2) = 2*0.6*0.6*0.4 = 0.288`

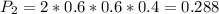
Finally

`P = P_(1) + P_(2) = 0.36 + 0.288 = 0.648`

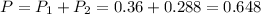
There is a 64.8% probability that the Cubs would win in a 2-out-of-3 series.