Question

An electron emitted in the beta decay of bismuth-210 has a mean kinetic energy of 390 keV. (a) Find the de Broglie wavelength of the electron. (b) Would such an electron be useful in a Davisson-Germer type scattering experiment? Address this question by determining the angle at which a first-order diffraction maximum would be found using the same nickel target as Davisson and Germer.

Answer 1

λ=1.7pm

This electron would not be useful in a Davisson-Germer type scattering experiment.

θ=0.45⁰

Step-by-step explanation:

a) We need to use the relativistic for of the kinetic energy:

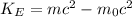`K_(E)=mc^(2)-m_(0)c^(2)`. (1)

Here m₀ is the mass rest and c the speed of light in vacuum.

We can write this equation in terms of the linear momentum (p) using this expression:
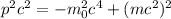`p^(2)c^(2)=-m_(0)^(2)c^(4)+(mc^(2))^(2)` (2)

if we solve this equation for p and put into the first equation we will have the KE in terms of p.

From (2) we have:
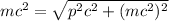`mc^(2)=\sqrt{p^(2)c^(2)+(mc^(2))^(2)}` (3)

Let's substitute mc² in (1).

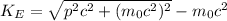`K_(E)=\sqrt{p^(2)c^(2)+(m_(0)c^(2))^(2)}-m_(0)c^(2)` (4)

Now, let's solve this for p:

`p=\frac{\sqrt{K_(E)(K_(E)+2m_(0)c^(2))} }{c}`

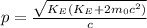
And finally, using the De Broglie wavelength equation
`\lambda=(h)/(p)=\frac{hc}{\sqrt{K_(E)(K_(E)+2m_(0)c^(2))}} =1.7*10^(-12)`.

`m_(0)c^(2)=0.511*10^(6)eV`

`h=4.136*10^(-15) eVs`

`c=3*10^(8)m/s`

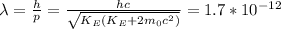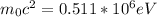
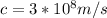
b) To determine the angle of the first order diffraction, we use the Bragg equation:

`n\lambda=dsin(\theta).`

Now , in the Davisson and Germer, they use a nickel target, so the inter atomic distance for this particular element is around 0.215 nm. We take n=1 for the first order

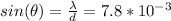`sin(\theta)=(\lambda)/(d)=7.8*10^(-3)` and
`\theta=0.45^(o)`.

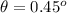If we see, this angle is to small to implement the experiment, so it would not be useful in a Davisson-Germer type scattering experiment.