Question

Peter's suitcase weighs 14 2/5 pounds, and he adds 3/5 pounds each minute. William's suitcase weighs 48 pounds, and he removes 4/5 pounds each minute. After how many minutes will the weight of both suitcases be the same?

Answer 1

After 25 minutes both bags of Peter's suitcase will have same weights.

Solution:

Given, Peter's suitcase weighs
`14 (2)/(5)=(14 * 5+2)/(5)=(72)/(5) \text { pounds }`

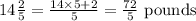
And he adds
`(3)/(5)` pounds each minute.

Then, series of his bag weights will be
`(72)/(5)+(3)/(5)+(3)/(5), \ldots \ldots \ldots \ldots`

This forms an Arithmetic progression
`\rightarrow (72)/(5), (75)/(5), (78)/(5), \ldots . \text { with first term } \mathrm{a}=(72)/(5) \text { and common difference } \mathrm{d}=(3)/(5)`

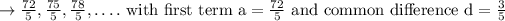
William's suitcase weighs 48 =
`(240)/(5)` pounds, and he removes
`(4)/(5)` pounds each minute.

Then, series of bag weights will be
`(240)/(5), (240)/(5)-(4)/(5), (240)/(5)-(4)/(5) \ldots \ldots \ldots \ldots \ldots \ldots`

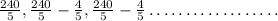
This forms an A.P
`\rightarrow (240)/(5), (236)/(5), (232)/(5), \ldots \ldots \text { with first term }=(240)/(5) \text { and common difference } \mathrm{d}=(-4)/(5)`

After how many minutes will the weight of both suitcases be the same?

So, now we have to equate nth terms of above two series to get the answer.

Then, nth term of peters series = nth term of Williams series

nth term = a + (n – 1)d

`\begin{array}{l}{(72)/(5)+(n-1) (3)/(5)=(240)/(5)+(n-1) (-4)/(5)} \\\\ {(n-1) (3)/(5)+(n-1) (4)/(5)=(240)/(5)-(72)/(5)} \\\\ {(n-1) (3+4)/(5)=(240-72)/(5)} \\\\ {(n-1) (3+4)/(5)=(240-72)/(5)} \\\\ {(n-1) (7)/(5)=(168)/(5)} \\\\ {(n-1) * 7=168} \\\\ {(n-1) * 7=168} \\\\ {n-1=(168)/(7)} \\\\ {n-1=24} \\\\ {n=24+1=25}\end{array}`

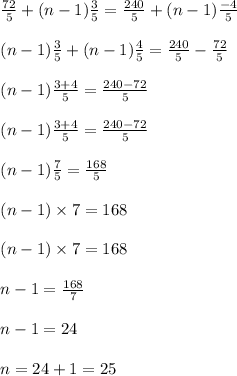
Hence after 25 minutes both bags will have same weights.