Question

70.0 kg ice hockey goalie, originally at rest, catches a 0.150 kg hockey puck slapped at him at a velocity of 35.0 m/s. Suppose the goalie and the ice puck have an elastic collision and the puck is reflected back in the direction from which it came. What is the final speed of the puck?

Answer 1

Answer: The final velocity of goalie and ice puck is 0.075 m/s in opposite direction

Step-by-step explanation:

To calculate the velocity of the goalie and ice puck after the collision, we use the equation of law of conservation of momentum, which is:

`m_1u_1+m_2u_2=(m_1+m_2)v`

where,

`m_1` = mass of goalie = 70.0 kg

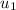`u_1` = Initial velocity of goalie = 0 m/s

`m_2` = mass of ice puck = 0.150 kg

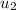`u_2` = Initial velocity of ice puck = 35.0 m/s

`v` = Final velocity of goalie and ice puck = ?

Putting values in above equation, we get:

`(70.0* 0)+(0.150* 35.0)=(70.0+0.150)v\\\\v=(5.25)/(70.150)=0.075m/s`

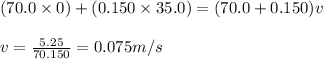
Hence, the velocity of goalie and ice puck is 0.075 m/s in opposite direction

Answer 2

v₂f = - 34.85 m/s

Step-by-step explanation:

If

m₁ = 70 Kg

m₂ = 0.150 kg

v₁i = 0 m/s

v₂i = 35 m/s

v₂f = ?

We can use the following equation (for an elastic collision):

v₂f = ((2m₁) / (m₁ + m₂)) v₁i + ((m₂ – m₁) / (m₁ + m₂)) v₂i

⇒ v₂f = ((2*70) / (70 + 0.15)) (0) + ((0.15 – 70) / (70 + 0.15)) (35)

⇒ v₂f = - 34.85 m/s