Answer with explanation:
As per given , we have
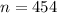
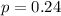
a) s per given , we have
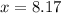

n= 64
a)Critical z-value for 99% confidence :
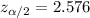
Confidence interval :
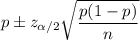
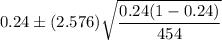
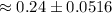
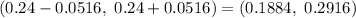
Hence, the 99% confidence interval for the population proportion of women who wear flat shoes to work =
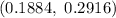
b) Margin of error : E= 0.01
Critical z-value for 95% confidence :
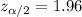
since , the prior estimate of proportion of women who wear athletic shoes to work is unknown.
Thus , sample size =
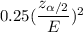
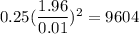
Required sample size : 9604