Question

Write the standard form of the line that passes through the given points. Include your work in your final answer. Type your answer in the box provided to submit your solution. (-3,5) and (-2,-6)

Answer 1

Answer: 11x + y +28 = 0

Explanation:

To find the equation of the line, we must first find the slope(m)

Given ; x₁= -3 y₁ = 5 x₂= -2 y₂= -6

slope(m) = y₂ - y₁ / x₂ - x₁

= -6-5 / -2-(-3)

= -11/(-2+3)

= -11

slope(m) = -11

We can now proceed to find tge equation.

Equation of a straight line is;

y - y₁ = m (x - x₁)

y - 5 = -11 (x --3)

y - 5 = -11 (x +3)

y - 5 = -11x - 33

y + 11x -5 +33 =0

y + 11x -28 =0

11x + y - 28 = 0

Answer 2

`\boxed{11x+y=-28}`

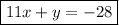
Explanation:

The 2-point form of the equation of a line is a good place to start. For points (x1, y1) and (x2, y2) that equation is ...

y = (y2 -y1)/(x2 -x1)(x -x1) + y1

Substituting the given points, we get ...

y = (-6 -5)/(-2-(-3))/(x -(-3)) +5

y = -11(x +3) +5 . . . . simplify

y = -11x -28 . . . . . . . eliminate parentheses

11x + y = -28 . . . . . . add 11x to put into standard form

___

The graph shows the given points and the equation in standard form.