Question

Which number can each term of the equation be multiplied by to eliminate the fractions before solving? m – negative StartFraction 3 Over 4 EndFraction m minus StartFraction one-half EndFraction equals 2 StartFraction one-fourth EndFraction m. = 2 + m 2 3 4

Answer 1

By multiplying each term by 4

Answer 2

"by multiplying each term by 4"

Step-by-step explanation:

Given

`-(3)/(4)m-(1)/(2)=2+(1)/(4)m`

The given equation is in the fraction form.

Now we need to find the least common factor that is the LCM.

Therefore,

`-(3)/(4)m-(1)/(2)=2+(1)/(4)m`

The least common multiple of the above terms is 4

Therefore by multiplying each term of the equation by 4, we get,

`\left (-(3)/(4)m* 4  \right )-\left ((1)/(2)* 4  \right )=\left (2* 4  \right )+\left ((1)/(4)m* 4  \right )`

`-3m-2 = 8+m`

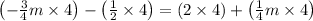
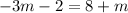
Thus by multiplying each terms by 4 we can eliminate the fraction.

Thus the answer is "by multiplying each term by 4"