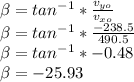Question

A spacecraft on its way to Mars has small rocket engines mounted on its hull; one on its left surface and one on its back surface. At a certain time, both engines turn on. The one on the left gives the spacecraft an acceleration component in the x direction of ax = 5.10 m/s2, while the one on the back gives an acceleration component in the y direction of ay = 7.30 m/s2. The engines turn off after firing for 645 s, at which point the spacecraft has velocity components of vx = 3780 m/s and vy = 4470 m/s. What was the magnitude and the direction of the spacecraft's initial velocity before the engines were turned on? Express the magnitude as m/s and the direction as an angle measured counterclockwise from the +x axis.

Answer 1

v=545.41
`(m)/(s)`

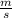
β=-25.93

Step-by-step explanation:

Give the acceleration in 'x' and 'y' also the time can find the initial velocity using equation of uniform acceleration motion

For axis x

`a_(x)=5.10(m)/(s^(2)) \\v_(fx)=3780(m)/(s) \\v_(fx)=v_(ox)+a_(x)*t\\v_(ox)=v_(fx)-a_(x)*t\\v_(ox)=3780 (m)/(s)-5.1(m)/(s^(2) )*645s\\v_(ox)=490.5(m)/(s)`

For axis y

`a_(y)=7.30(m)/(s^(2)) \\v_(fy)=4470(m)/(s) \\v_(fy)=v_(oy)+a_(y)*t\\v_(oy)=v_(fy)-a_(y)*t\\v_(oy)=4470(m)/(s)-7.30(m)/(s^(2) )*645s\\v_(oy)=-238.5(m)/(s)`

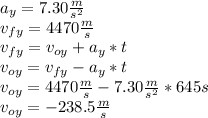
Maginuted

`v=\sqrt{v_(xo)^(2) +v_(yo)^(2) } \\v=\sqrt{490.5x^(2) +(-238.5)^(2) }\\v=545.41 (m)/(s)`

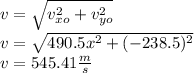
The direction is knowing when find the angle so

`\beta =tan^(-1)*(v_(yo) )/(v_(xo))\\\beta =tan^(-1)*(-238.5)/(490.5)\\\beta =tan^(-1)*-0.48\\\beta =-25.93`