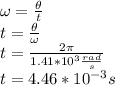Answer:
(a)
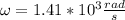
(b)
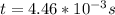
Step-by-step explanation:
The angular speed is a measure of the rotation speed. Thus, It is defined as the angle rotated by a unit of time:
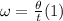
The arc length in a circle is given by:

s is the length of an arc of the circle, so
 .
.
Replacing (2) in (1):

a) Now, we calculate the angular speed:
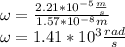
b) We use (1) to calculate the time it takes to make one revolution, which means that
 is
is
 .
.