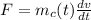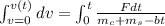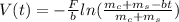Question

A freight car of mass M contains a mass of sand m. At t = 0 a constant horizontal force F is applied in the direction of rolling and at the same time a port in the bottom is opened to let the sand flow out at constant rate dm/dt. Find the speed of the freight car when all the sand is gone. Assume the freight car is at rest at t = 0.

Answer 1

Amount of linear movement

Step-by-step explanation:

Our system is defined by the rate of change in mass that

leaves the car
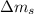`\Delta m_ {s}` , this happens during a time interval

`[t, t + \Delta t]`, in addition to freight car and sand at time t.

In this way we need to define the two states:

State 1,

consider
`t, m_ {c} (t) + \Delta m_ {s}` and V.

State 2,

consider
`t + \Delta t, m_ {c} (t), V + V \Delta V`

In this state is the mass of sand output, which

is composed of

`\Delta m_(s), V + \Delta V`

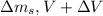
In this way we define the Linear movement in x, like this:

`p_ {x} (t) = (\Delta m_ {s} + m_ {c} (t)) v`

`p_ {x} (t+\Delta t) = (\Delta m_ {s} + m_ {c} (t)) (v + \Delta v)`

`m_ {c} (t) = m_ {c, 0} - bt = m_ {c} + m_ {s} -bt`

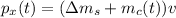
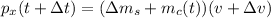
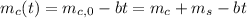
In this way we proceed to obtain the Force

`F =\lim_(\Delta t \rightarrow 0) \frac {p_x (t + \Delta t) -p_ {x} (t)} {\Delta t}`

`F = lim_(\Delta t \rightarrow 0) m_ {c} (t) \frac {\Delta v} {\Delta t} + lim_(\Delta t \rightarrow 0) m_ {s} (t) \frac {\Delta v} {\Delta T}`

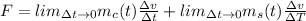
Since the mass of the second term becomes 0, the same term is eliminated, thus,

`F = m_ {c} (t) \frac {dv} {dt}`

`\int\limit ^ {v (t)} _ {v = 0} dv = \int\limit^t_0 \frac{Fdt} {m_ {c} + m_ {s} -bt}`

`V (t) = - \frac {F} {b} ln (\frac {m_c + m_s-bt} {m_c + m_s})`